Сложение колебаний
При сложении двух колебаний синусоидальной формы
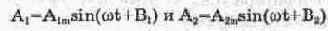
образуется синусоидальный сигнал той же частоты
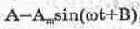
где
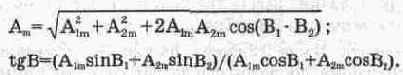
Следует заметить, что формула для А„ справедлива как для амплитудного, так и эффективного значения тока и напряжения, в чем нетрудно убедиться, подставив в эту формулу эффективные значения А,„и Аа„. Это замечание связано с тем, что далее мы будем пользоваться именно эффективными значениями токов, взятыми в данном случае из схемы на рис. 6.1.
Определим в качестве примера сумму и разность двух синусоидальных токов
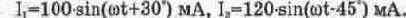
Используя приведенные выше формулы. лля СУММЫ токов ПОЛУЧИМ:
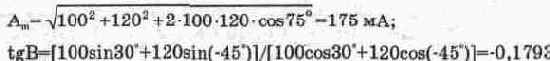
откуда фаза В=-10'10'.
Для вычисления разности токов воспользуемся соотношением:
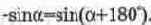
В этом случае вычитаемый ток
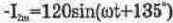
. Таким образом, задача вычитания второго тока из первого сводится к суммированию с учетом проделанных преобразований. Для разности токов в таком случае получим:
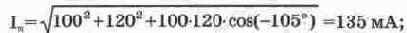
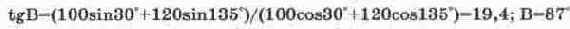
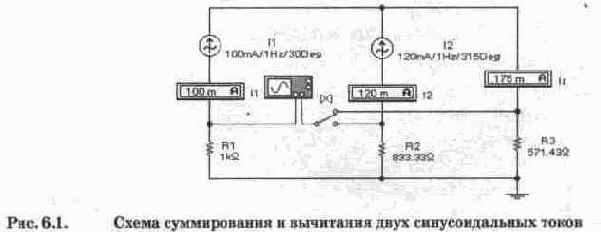
Схема для моделирования суммирования и вычитания синусоидальных токов показана на рис. 6.1. В ней использован источник переменного тока, в диалоговом окне которого можно задать частоту, ток и фазу в градусах. Однако задавать отрицательные значения фазы в программе не допускается. Поэтому для тока 12 задана начальная фаза 315°, поскольку sin(-45°)=sin(360°-45°). Для измерения токов в каждую ветвь включены амперметры в режиме измерения переменного тока (АС). Как видно из показаний амперметра, измеряющего ток Is, результаты суммирования токов совпадают с результатами расчетов.
Для измерения фазы использован осциллограф, в канале А которого регистрируется сигнал от источника II, создающий на резисторе R1 падение напряжение I1-R1=0,1-1000=100 В. Канал В осциллографа с помощью ключа Х может подключаться к резисторам R2, R3, сопротивления которых рассчитаны таким образом, чтобы токи II, Is создавали на них падения напряжения тоже 100 В (для удобства проведения осциллографических измерений). Пользуясь переключателем X, можно контролировать фазовые соотношения между токами II, 12, Is. В положении переключателя, показанном на рис. 6.1, такие соотношения можно регистрировать между токами II, Is.
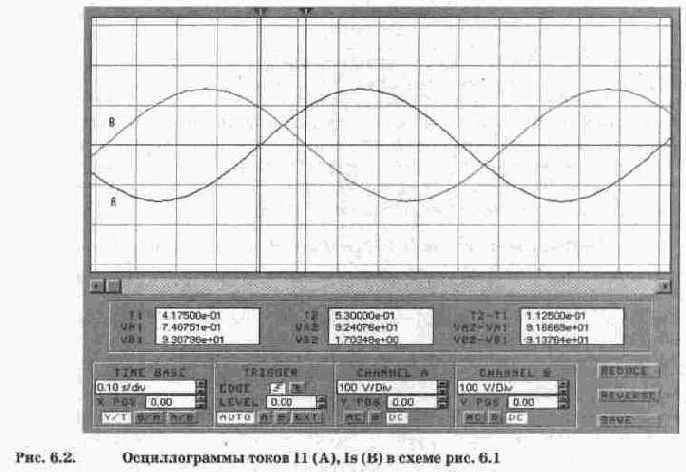
Результаты осциллографических измерений, полученные при моделировании процесса суммирования двух синусоидальных токов, показаны на рис. 6.2 (для повышения точности отсчета осциллограф включен в режиме ZOOM). Визирные линии поставлены в точки пересечения синусоидами оси времени (визирная линия 1 — для тока II, 2 — для тока Is). Из правого цифрового табло отсчетов видно, что временной промежуток между визирными линиями составляет Т2-Т1=0,1125 с. Поскольку период колебаний исследуемых сигналов составляет Т=1 с (частота 1 Гц), то измеренный промежуток времени, пропорциональный разности начальных фаз токов II, Is, в градусах может быть определен из очевидного соотношения:
В1-В=360°(Т2-Т1)/Т=360(0,1125)/1=40,5°=40°30', откуда фаза суммарного тока В=-10°30', что отличается от расчетного на 19'. Эта разница (около 3%) объясняется погрешностью отсчета временного интервала при установке визирных линий (так называемая погрешность параллакса).
Результаты моделирования вычитания токов приведены на рис. 6.3, откуда видно, что они полностью совпадают с данными расчета. Обратите внимание, в схе-
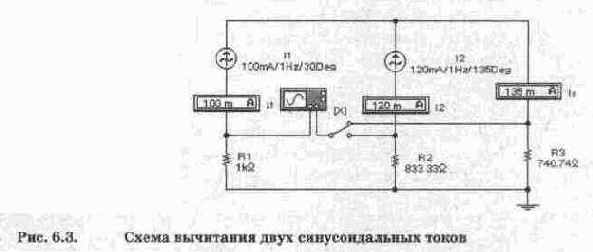
ме сопротивление резистора R3 изменено для удобства проведения осциллографических измерений.
Рассмотрим теперь сложение напряжений
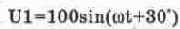
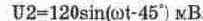
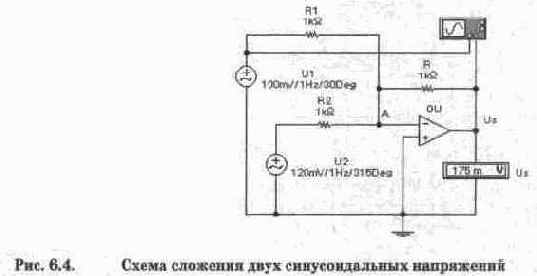
Схема измерений для этого случая показана на рис. 6.4. Она выполнена в виде суммирующего устройства на операционном усилителе OU. Коэффициент передачи для каждого источника напряжения равен R/R1=R/R2=1 (см. гл. 10). По существу с помощью суммирующего усилителя процесс сложения напряжений сведен к процессу суммирования токов I1=U1/R1 и I2=U2/R2 на резисторе R. При этом справедливость приведенных формул обеспечивается тем, что потенциал точки А за счет большого коэффициента усиления ОУ практически равен нулю.
Контрольные вопросы и задания
1. Почему методы расчета цепей постоянного тока нельзя использовать для расчета цепей переменного тока? В каких случаях это можно делать?
2. Проведите расчеты и моделирование сложения двух синусоидальных токов при разности фаз токов 60°.
3. Проведите анализ фазовых соотношений в схеме на рис. 6.3 по результатам моделирования.
4. С помощью осциллографа измерьте фазу суммарного напряжения в схеме на рис. 6.4.
