Функции 4-х переменных
Для функций 4-х переменных применяются диаграммы следующего вида:
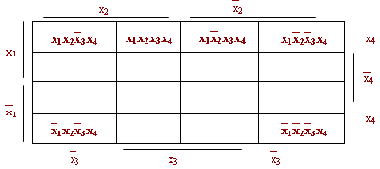
Все, что было сказано относительно функций 2-х, 3-х переменных справедливо и в данном случае. Но данная диаграмма обладает дополнительной особенностью: при поиске минимальной формы функции необходимо считать склееными правый край с левым и верхний с нижним.
Говорят, что для удобства целесообразно считать данную диаграмму написанной на поверхность тора.
Пример:
f(x1,x2,x3,x4) = x1x2x3x4




x1x2x3x4

Составим диаграмму:
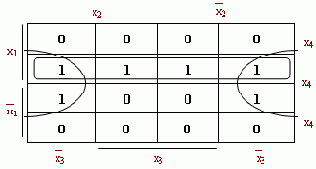
fmin(x1,x2,x3,x4) = x1x4

Заметим, что на основании свойства диаграммы четыре единицы, стоящие в угловых клетках диаграммы соответствуют конституентам, которые склеиваются между собой.
Итак, дадим формализированное описание метода.
Опредение. Правильной конфигурацией ранга К называется совокупность единиц (нулей), образующая прямоугольник площадью 2к.
Для минимизации функции, зависящей от n аргументов, отыскиваются правильные конфигурации вначале n-1 ранга, затем n-2 ранга и т.д.
Далее определяется накрытие найденных правильных конфигураций совместной проекцией соответствующих строк и столбцов, которая выделяет данную правильную конфигурацию.
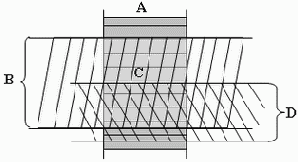
Рис. 4.1. Определение правильных конфигураций
C– правильная конфигурация
A,B,D– проекции конфигурации
А*В– результат склеек
